Learn in this article how to create elliptic curve (EC) keys for your public key infrastructure (PKI) and your certificate authority (CA). We will use the Elliptic Curve Diffie Hellman (ECDH) as keyagreement along with Elliptic Curve Digital Signature Algorithm (ECDSA) for signing/verifying.
Table of Contents
1. Why was Elliptic Curve Cryptography (ECC) invented?
The common way for cryptography was RSA before ECC was introduced into the ASN standard.
RSA is based on factorization of large prime factors. The longer the prime number the more secure is the cryptography. But the drawback of long prime numbers is the high CPU load and especially long encryption and decryption time. To create a 3072 bit RSA keypair will cost multiple seconds on modern hardware. Compared to this a 256 bit EC keypair is generated in a twinkling of an eye. As a thumb of rule you can say a 256 bit EC public key provides comparable security as a 3072 bit RSA public key.
Also there was a big need to reduce CPU usage for encryption with the evolving smartphone market. Also the block-chains need for fast encryption was one big driver for the success of the new elliptic curve approach.
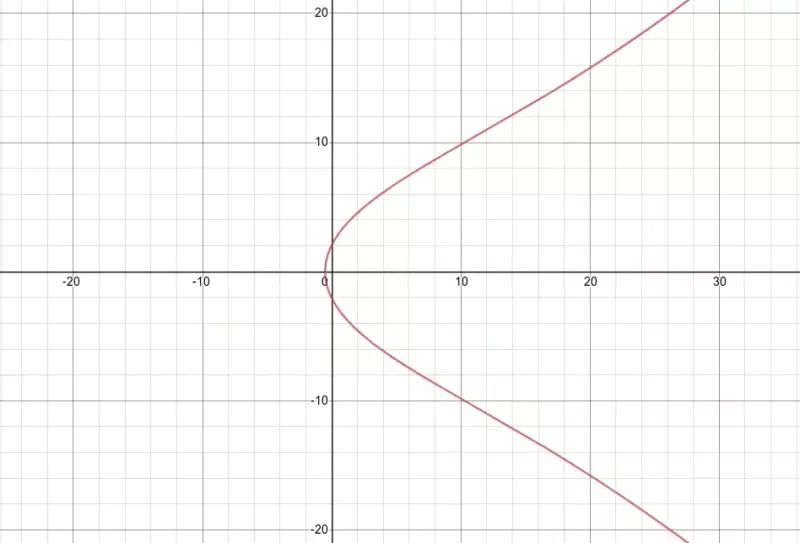
2. Introduction to elliptic curves
As mentioned before RSA consists of prime factors there ECC consists of elliptic curves with defined points on the curve. To understand elliptic curves better, lets start with a simple graph.
2.1. Example of an elliptic curve
In the following animation you see the equatation
y² = x³ + ax + 4
with varying a
So you can see, that such a simple equatation creates very odd - in my oppinion beautiful - graphs. Elliptic cryptography curves therefore follow this generic equatation:
y² = x³ + ax + b
In the equatation you see the coordinates x and y along with the so called domain parameters a and b.
To shorten the scientifical part here, lets sum up the rules for elliptic curves:
- all Points in a curve satisfy an equation, and thus can be calculated
- knowing “x” you will ultimately know “y”
- The curve is symmetric to the Y-axis
- Domain parameters affect various attributes of a given elliptic curve
- If a straight line intersect two points of the elliptic curve, the line will also intersect a third one
So knowing all this gives a brief introduction of how from knowing two points your third point can be calculated. The third point represents your public key.
3. Recommendations on key lengths
Known security organizations have recommendations and comparisons on key lengths. Their recommendation does not mean that you have to use the keysize of the specific timeframe. It is more or less a recommendation to ensure, that you information stay protected. If you choose already longer keylength you are on the more secure side on keeping information private.
3.1. US NIST recommendation 2016
| recommended till | Symmetric | prime | elliptic | hash |
| up to 2016 | 80 | 1024 | 160 | 160 |
| 2016 - 2030 | 112 | 2048 | 224 | 224 |
| 2016 - 2030 and beyond | 128 | 3072 | 256 | 256 |
| 2016 - 2030 and beyond | 192 | 7680 | 384 | 384 |
| 2016 - 2030 and beyond | 256 | 15360 | 512 | 512 |
3.2. German BSI recommendation 2018
| recommended till | Symmetric | prime | elliptic | hash |
| 2018 - 2022 | 128 | 2000 | 250 | 256 |
| 2023 - 2024 | 192 | 3000 | 250 | 384 |
4. What is a ECDH?
ECDH stands for Elliptic Curve Diffie-Hellman and defines a key exchange protocol. This protocol is used to establish a shared secret key for encryption without the need sending it directly to each other. To avoid too much maths here, we will glance through the key exchange protocol:
- a set of domain parameters get exchanged between the communication partners (sideA and sideB)
- sideA generates a private and public key with the given domain parameters
- sideB generates also a private and a public key with the given domain parameters
- both sides now exchange their public keys
- sideA now calculates with the public key of sideB and the initally shared function a new a shared secret, also known as a derived key dkB
- sideB does the same with the public key of sideA and the initially shared function and gets a shared secret (derived key dkA)
- sideA can now use the derived key dkB to encrypt a message
- sideB can also use the derived key dkA to also encrypt a message
- both sides can now easily decrypt the messages with their own private keys
5. How to create ECDH keys?
Now get the hands on the keyboard to create some keypairs. We will need openssl for this and a bash shell (cygwin or a *NIX system).
To check what openssl supports on your machine execute:
openssl ecparam -list_curves
In our examples we will use the prime256v1.
5.1. The fast path for creating the keypair
openssl ecparam -name prime256v1 -genkey -noout -out $HOME/mykey-prime256v1.pem
generates something like this:
-----BEGIN EC PRIVATE KEY-----
MHcCAQEEIJ+lSQBRbe1tyyZ4zctO+NOunDMVbquGOfrbiM8IybvQoAoGCCqGSM49
AwEHoUQDQgAEtHqNA4i3DDx0ey8nYhUVTArVZpzBzq2A2AR0X3VVy8VA3M49RYJm
rqw7hPM4ywIetVhNUw4+qEP7mV5tPXFcxw==
-----END EC PRIVATE KEY-----
now let us see the EC parameter details of our key
openssl ec -in $HOME/mykey-prime256v1.pem -text -noout
generates something like this
read EC key
Private-Key: (256 bit)
priv:
00:9f:a5:49:00:51:6d:ed:6d:cb:26:78:cd:cb:4e:
f8:d3:ae:9c:33:15:6e:ab:86:39:fa:db:88:cf:08:
c9:bb:d0
pub:
04:b4:7a:8d:03:88:b7:0c:3c:74:7b:2f:27:62:15:
15:4c:0a:d5:66:9c:c1:ce:ad:80:d8:04:74:5f:75:
55:cb:c5:40:dc:ce:3d:45:82:66:ae:ac:3b:84:f3:
38:cb:02:1e:b5:58:4d:53:0e:3e:a8:43:fb:99:5e:
6d:3d:71:5c:c7
ASN1 OID: prime256v1
NIST CURVE: P-256
5.2. The longer way to create a keypair
To create our keypair we will need the EC parameters (including the domain parameters) for our elliptic curve. Let us generate a set of it
openssl ecparam -name prime256v1 -out $HOME/prime256v1-ecparams.pem
cat /tmp/mykeypair-prime256v1-ecparams.pem
generates something like this:
-----BEGIN EC PARAMETERS-----
BggqhkjOPQMBBw==
-----END EC PARAMETERS-----
now use this file to create our keypair
openssl ecparam -in $HOME/prime256v1-ecparams.pem -genkey -noout -out $HOME/mykeypair-prime256v1.pem


